VIGRE/GT REU Summer 2006 Mini Conference

THURSDAY, JULY 27, 2006

Discrete Biorthogonal Polynomials
by Beth Hart (School of Mathematics, Georgia Tech)

We have been analyzing discrete biorthogonal polynomials, which generalize the notion of discrete orthogonal polynomials. Our polynomials P_n of degree n satisfy a biorthogonality relation such as \sum_{j=0}^\infty {P_n(x_j)(\psi (x_j))^k w(x_j)} = 0, for k = 0,1,...,n-1. Here x_0,x_1,... is a sequence of points, the weight w is positive on all these points, and \psi is an increasing function on an interval containing all x_j. The special case \psi (x) = x generates discrete orthogonal polynomials. We investigate expicit formulae for P_n for various choices of \psi, x_j, and w.
REU Mentor: Doron Lubinsky

Alexandrov's Conjecture: Intrinsic diameter and area of convex surfaces
by Brian Nakamura (School of Mathematics, Georgia Tech)

This 50 year old conjecture by Alexandrov has commonly been cited, yet there are very few known results. An introduction to the conjecture and some recent progress will be presented. A few observations and partial results produced during the summer REU will also be discussed.
REU Mentor: Mohammad Ghomi

The Homology of 17-Crossing Knots: A Computational Approach to Knot Theory
by Darshan Bryner (School of Mathematics, Georgia Tech)

Knot Theory is a relatively new field in Mathematics, and hence many mathematical properties of knots remain unfounded. To date, a comprehensive list of all knots without repetitions of up to only 16 crossings exists. In this research project, Lew, Stavros, and I have created a database to store knots of up to 17 crossings and implemented a program to hopefully form the most accurate list in existence of such knots without repetitions. My talk will address knot theory terminology and definitions, the software tools used in our computation, the structure of our database, and the use of parallel processors to achieve the necessary computational power.
REU Mentor: Lew Lefton

Time-Optimal Control of Bioterror Response Logistics: The Case of Anthrax
by Andrew Brown (Biology, Georgia Tech)

This project begins the analysis of optimal control of bioterror response logistics. The necessary conditions for time-optimal control are given, based on the calculus of variations and dynamic programming. A gradient algorithm is implemented and used to test the queueing network model as well as the algorithm's own reliability. Experimental simulation results are presented and discussed.
REU Mentor: Shui-Nee Chow

The Four Vertex Theorem and the Extension of its Converse to the Sphere
by Bobby DeMarco (University of Delaware)

Adolf Knesser proved in 1912 that any simple closed planar curve has at least four vertices, or points of maximum or minimum curvature. Over the past almost hundred years many versions and extensions of this theorem have been explored. Notably, in 1971 Herman Gluck proved a type of converse to the four vertex theorem. Gluck showed that given a strictly positive curvature function with at least four vertices, it is possible to construct a simple closed planar curve as a function of time, t, such that the curvature at any point on this curve corresponds to the given curvature function. This presentation will discuss the continuation of Gluck's work and examine how Professor Ghomi and I hope to extend it to the sphere.
REU Mentor: Mohammd Ghomi

An Analysis of the Three Hat Problem
by Brian Benson (School of Mathematics, Georgia Tech)

In 2003, the Three Hat Problem written by Donald Aucamp appeared in MIT's Technology Review. The puzzle gives a scenario in which three people wearing hats are sitting together and each hat can be seen by everyone except the person that is wearing that hat. Each person is told that all of the hats contain a positive integer and that two of the integers add to the third. In an ordered, turn-wise, modular fashion, each person truthfully states whether or not he knows his number. We present a mathematical method by which to analyze all positive integer cases of the Three Hat Problem puzzle. Using this analysis, we show how and why it is always the case that one of the three people can figure out the integer that is on his hat. Further, we give a simple algorithm to derive the dialogue for any case and ordering of three integers that might occur in the puzzle.
REU Mentor: Yang Wang

Searching for Periodicity in the Game of Officers
by Garret Thompson (Computer Science, Georgia Tech)

A taking-and-breaking game is played by removing beans from a heap and then splitting what remains into new heaps, where the number of beans removed and the number of heaps depend on the rules of the game. According to the Sprague-Grundy theorem, each position in such a game is equivalent to a position in a simpler game called Nim, and if you can determine a function mapping heap sizes to "Nim-values," you can play the game optimally. It is conjectured that this function is periodic for most taking-and-breaking games, and we explore techniques that have been used to solve other games, applying them to a specific game called Officers.
REU Mentor: Tom Morley

An algebraic approach to a graph choosability problem

by Masanori Koyama (Harvey Mudd College)
A graph is called n-list colorable if for every family of sets S_v (v in G) with |S_v| =k for all v, there exists a proper coloring of the graph such that each v is colored from the colors in S_v. The smallest n such that the graph G is n-list colorable is called the choosability of G and is denoted ch(G). It is known that \chi(L(G)) = ch(L(G)) =3 for 2-connected cubic planar graphs. It is not known if this holds for cubic non-planar graphs, although it is known to hold for K_{3,3}. Using an algebraic method, attempt was made to show the 3 edge-choosability of K_{3,3} with vertices replaced with triangles.
REU Mentor: Robin Thomas

On the Abel-Jacobi Map from a Graph to its Jacobian
by Dragos Ilas (Physics, Georgia Tech)

There is a natural way to attach to any graph a finite Abelian group called the Jacobian group, or Picard group, of the graph. There is also a natural map from the graph to its Jacobian group called the Abel-Jacobi map. A program was written to calculate the Jacobian group and the Abel-Jacobi map using the Smith Normal Form. We discuss some conjectures and theorems about the injectivity and surjectivity of powers of the Abel-Jacobi map. The latter is related to the number of linearly independent cycles which the graph possesses. Finally, we investigate the relationship of these questions to a certain chip-firing game on graphs.
REU Mentor: Matt Baker

Markov Chains and Traffic Analysis
by Emanuel Indrei (School of Mathematics, Georgia Tech)

In this study, we use Markov chains to construct a theoretical traffic system. The presentation is organized into three major parts: The first two deal with the construction of two spaces in which objects may interact. The third part analyzes the evolution of one particular object. Using the central limit theorem and bounds given by the law of iterated logarithm, we prove that after a large number of time steps, the probability of locating this object in the traffic network diminishes to zero. We conclude by offering methods of analyzing the evolution and interaction of multiple objects and accounting for accidents.
REU Mentor: Tom Morley

GOEDEL
by Lee Martie (Computer Science, Georgia Tech)

The GOEDEL program, Belinfante's computer implementation of Kurt Godel's algorithm for class formation in Mathematica, was used to formulate definitions and theorems in the theory of relations, abstract algebra and arithmetic. The ultimate goal would be to use the results derived to obtain automated proofs using McCune's automated reasoning program Otter. The specific focus of this research was to translate into the language of the GOEDEL program the formulation of Peano arithmetic in terms of unary algebras as expounded by Birkhoff and Bartee in their book on Modern Applied Algebra. Several Mathematica notebooks were prepared and posted on the web, detailing some of the more interesting results obtained in the course of this work. The first notebook dealt with the class UNOPS of all unary operations. A unary operation is a function whose range is contained in its domain. General properties of this class were derived, and examples of unary operations were provided. The second notebook posted was about partial orders and equivalence relations. In this notebook, direct proofs were obtained for results that had initially been found using reification, a procedure for associating relations to constructors. The third notebook was about a theorem concerning unions of commuting transitive relations. Two notebooks were posted about powers of unary operations. A formula for the class of mappings with one-point domains was derived, as a first step toward proving theorems about mappings using induction on the size of their domains. The final topic studied concerned cyclic unary algebras, and the clock algebra in particular.
REU Mentor: Johan Belinfante

Distinguishing Legendrian Knots
by Gokhan Civan (School of Math and Aerospace Engineering, Georgia Tech)

Legendrian knots are knots that satisfy certain geometric properties. There are various algebraic invariants that are used to differentiate between Legendrian knots. Recently a very complicated invariant in the form of a differential graded algebra was discovered. There are also invariants that are derived from this more general invariant through a process of linearization. There are open questions about the equivalence or relative strengths of these derived invariants. This research consisted of investigating examples in hopes of shedding light onto some of these questions. The effort has been assisted by a Mathematica code which has been developed along the way and could culminate in a general tool to compute some of these invariants for Legendrian knots.
REU Mentor: John Etnyre

A Mathematical Framework for Paper Folding
by Steven Britt and Laura Stiltz (School of Mathematics, Georgia Tech)

Our research has focused on utilizing the standard ideas of differential geometry to mathematically describe the notions associated with paper folding. We define folding functions both along lines, as is traditionally associated with folding, as well as more generally along planar curves. We then prove the intuitively necessary condition that any folding as we have defined is isometric to a plane. Further questions arise upon examination of the processes by which the paper is folded as a function of time. We also present a few examples, conjectures, and proofs on various topics in paper folding.
REU Mentor: John McCuan

VIGRE/GT REU Summer 2004

Summer 2004 GT REUs

Professor Student Topic

Robin Thomas Matt Perry Topics in Graph Theory

Mason Porter, Bunimovich Julie Bjornstad
Alexie Dachevski Mathematical Biology (See Below)

Hou Min Zhow Robert Pruvenok Image Processing

Shui Nee Chow Caroline Seabrook
Stephanie Chung Pattern Formation

Ernie Croot Bayazid Sarkar Fermat Numbers

Dana Randall Brittany Hughes Markov Chains

John McCuan Jeffrey Elms Soap Films in Corners

Example Topics

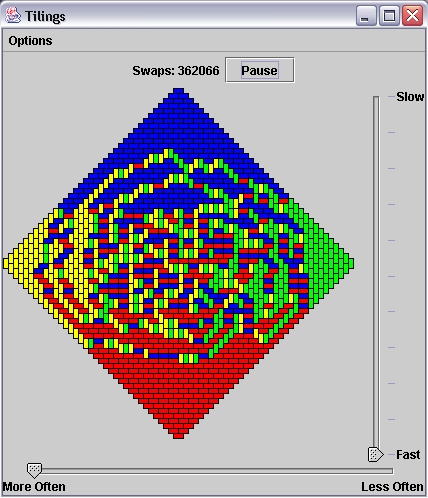Brittany Hughes: "The Effects of Boundry Conditions on Convergence Rates of Markov Chains" As an introduction to Markov Chains, I will study tilings of a N x N chess board. As the summer progresses, I will move onto perfect matchings on the square octogon lattice. I will also be studying how changing the boundry of a lattice will alter the mixing speed of a Markov Chain.

Food chains in phytoplankton (joint with Christopher Klausmeier, Dept of Biology)

Description: Theoretical ecology has a long mathematical tradition going back to Lotka and Volterra's predator-prey models. The student who undertakes this project will study a (3-species) food chain in phytoplankton with seasonal variation. (This generalizes recent work by Prof. Klausmeier and his collaborators.)

VIGRE/GT REU Summer 2003

Aug 14, 2003: Check back soon for a more detailed report about the REU activities this past summer. The range of activities, and their accomplishments, is, I think, impressive.


Summer 2003 GT REUs
Professor	Student	Topic
Robin Thomas	Michael Abraham	Topics in Graph Theory
Professor Mucha	Casey Warmbrand	Political Network Theory
Professor Mucha	Thomas Callaghan	Football Network Theory
Shui-Nee Chow and Mason Porter (Use email to contact Professor Porter.)	Jeremy Corbett	Numerical Work in Spatial Temporal Chaos.
Mason Porter	Steven Lansel	Computer Simulation of Billiard Systems
Michael Lacey	Brandon Luders, Alex Charis	Additive Number Theory

February 2004 Update

Steven Lansel, directed by Mason Porter Quoting: My project deals with billiard systems. A billiard system consists of a closed shape inside which a point particle bounces around. The point particle always travels at the same speed and bounces off the barrier of the billiard table with its angle of incidence equal to its angle of reflection. Depending on the shape of the billiard table, chaos or chaotic regions may be present in the system.

I am writing a program to simulate billiard systems to be used a tool for anyone working on them. The user is able to either select a billiard table from a list of the most commonly studied tables or enter an arbitrary shape and initial conditions. The program calculates the path of the point particle and plots the data in configuration and phase space.

Steven has continued his project into the fall and spring terms, refining the simulations, especially in the length of the paths of the balls. The code and many pretty pictures are freely available.

Casey Warmbrand, directed by Peter Mucha (Casey is also working with the supervision of a political science prof.) Quoting: I've been researching the network properties of the House of Representatives. Ive taken data for the past 8 congresses and created adjacency matrices. We have three types of matrices, one that contains congressmen and committees as the nodes, and a connection is defined between a person and committee if they serve on the committee, this type of network is bipartite. The other two types are projections of the first, one is people to people who are connected if they share a committee with the person, the other is committee to committee.

We've calculated a lot of basic network statistics; shortest/average path length, clustering coefficients, degree distributions and diameters. We've also created a community structure for each of the projections. The next things to look at will be, the removal of the subcommittees and taking the graph to only contain all the congressmen and the 19 standing committees, and recomputing some of the already calculated statistics and seeing what changes and if any trends are more readily apparent.

Attached is community structure of the committees (people are removed and disconnections are shown), also a nice trend is apparent in the degree distribution of the past 5 congresses (since the republicans took power).

Casey Warmbrand worked on his senior project on fractals in the Fall 2003 semester. In the spring semester, he has been one of three GT people in Budapest, studying math and computer science. The others are fellow GT undergrad David Eger, and the third is Adam Marcus, who will start graduate school at GT in the Fall 2004 semester.

Thomas Callaghan, directed by Peter Mucha Quoting: My REU titled "Football Network Theory" has been an examination of the current ranking schemes used for football and other sports and then the development of a simple yet innovative new scheme which takes into account the network properties inherent in the college football season. In addition to developing and examining our new system, I have also examined many different properties of the graph created by a college football schedule where teams are represented by vertices and games between two teams are represented by edges connecting the two vertices. Some of these properties include connectedness, clustering, community structure, betweenness, degree distribution, diameter, and the "small world'' phenomenon.

Go to the Directory Ring.jpg is simply a visual of the college football graph. Commstruct.jpg is a visual of the community structure of the graph generated using the latest community structure algorithm. If you closely examine, you will notice that it accurately places teams in the same conference together. The last file is a ranking of the NCAA Division IA football teams in 1990 (the last year Georgia Tech won the National Championship).

Thomas Callaghan has been continuing his work on this project into the Fall and Spring semesters. The article describing the particulars of this work is at the arXiv . The appearance of the article attracted attention from ESPN, Nature Online, the Chronicle of Higher Education. An article for the Notices of the American Mathematical Society is in preparation.

Brandon Luders, directed by Michael Lacey is developing some random models for Pollard's rho method for factoring. This delightful method, has a heuristic expected running time that is the square root of the smallest prime factor of the integer one is seeking to factor. The goal is to find some good probabilistic models for this method, and find a good estimate for the standard deviation of the running time.

Brandon Luders also continued his research topic into the Fall semester. He carried out extensive computations on the mean and standard deviation of the Pollard rho method. He discovered an anomalous deviation of the method from expected behaviors in a certain range of primes. His calculations conclusively show that the standard deviations are rather big, essentially as big as possible. An article should appear at the arXiv soon.

Alex Charis (a University of Toronto student) spent the summer investigating some aspects of number theory in both a computational and theoretical fashion. The questions pertained to the existence of certain presumably very rare primes. He has a nice report on his activities here.

Jessica Snyder worked on a problem in mathematical biology, specifically, a dynamical system model for some aspects of bipolar disorder, and in particular the effects of medication on the disease. This continued an ongoing research project of Mason Porter. Jessica Snyder reported on this project at the Dynamical Days meeting in January. The paper attracted a nice bit of attention, due to the novelty the approach.

Andrew Stimpson worked in an area of topology with a relation to the Hairy Ball theorem, and a very strong combinatorial aspect. He has a 12 page report on the subject, with an impressive array of figures in it.

Jeremy Corbett worked in the area of pattern formation in the solutions of partial differential equations. The physical model is a familiar one, if you take some sand in a box, and shake it rhthmyically, the sand will fall into some sort of pattern. The physics and mathematics of the problem is very interesting. And Jeremy Corbett spent the summer studying one research paper in the subject, and through the simulations, creating some very nice graphics that appear at differnt points in this web site.

He was joined by high school student A Behram who started at MIT in Fall 2004.

Ryan Hynd, not in the REU program, is in Leipzig Germany this summer, studying issues related to capillary surfaces. He and Professor McCuan have recent completed a paper on Rolling Curves, which grew out of last summer's investigations and experiments on Plateau's rolling drops. You can see movies of the same at the ACE Lab site. Ryan reported these results at a Sigma Xi conference in Los Angeles in December 2003.

Derrick Coetzee (not in the REU program) has written a program to turn Professor Belinfante's automatically generated proofs into humanly readable LaTex Output. The Lisp code is freely availible.

Blair Dowling directed by Dana Randall, is continuing the development of the stochastic model of the spread of HIV in the human body. This summer she is on the payroll of Emory Medical School. An abstract of a talk she gave at Microsoft Research on the subject.

Nathan Bell, directed by Peter Mucha is continuing to develop methods of simulating balls falling in an hour glass, and falling down a series of ramps. There are pics of 8000 balls falling down a series of ramps. Everything looks great. And is a fantastic job for his senior project. Check out the latest screen shots.

VIGRE/GT REU Summer 2002

The final report on the 2002 VIGRE/GT is availible.


Summer 2002 GT REUs
Professor	Student	Topic
Peter Mucha	Michael Abraham	Small World Networks, on the Bewoulf Cluster
John McCuan	Roberto Lopez	ACE Lab, Electrostatics
John McCuan	Jeffery Elms	ACE Lab, Electrostatics
John Pelesko	Ryan Hynd	ACE Lab, Electromagnetics
Joe Landsberg	Erika Norenberg	Morse Theory
Joe Landsberg	Joe Montgomery	Degenerate Gauss Maps on Algebraic Varieties
Johan Belinfante	David Eger	Artificial Intelligence
Xingxing Yu	Jeremy Barrett	Algebraic and Topological Aspects of Graphs
Prasad Tetali	David Skoog	Random Codes
Margeret Symington	Andy Wand	Contact Topology
Anthony Yezzi	Ganesh Sundaramoorthi	Electrostatics Charge, Image Segmentation
Prasad Tetali	Boris Kerzhner	Random Codes

Professor Peter Mucha's interests are in computation and fluids. He and Lew Lefton, the IT Director, have built a Beowulf cluster. What is that? It is a Linux supercomputer, is the short answer.

Michael Abraham's project is: Statistics of Evolving Scale Free and Small World Networks. Using the Beowoulf Cluster, he seeks to develop codes to study the connectivity of such networks, for comparison with theories in development by Professor Mucha.

The topic of Joe Montgomery's REU is " Classification of varieties with degenerate Gauss maps."

Given a surface in Euclidean three space, one can define its Gauss map, taking a point to its normal line translated to the origin, or equivalently, a point to its tangent space in the Grassmanian. In the analytic category, surfaces with degenerate Gauss maps (that is, where the image is one-dimensional) have been completely classified, they are either cones over a point or the union of tangent lines to a curve. The same question in higher dimensions and codimensions is open. Montgomery will work on this open question, building on the classification results of Griffiths-Harris, and Akivis-Goldberg for complex subvarieties of projective space with degenerate Gauss maps.

Ryan Hynd and Professor Pelesko will design and build an experimental apparatus to study the electrostatic deflection of soap films. We will construct and analyze a mathematical model of the experiment and compare experimental results with theory. Techniques in ordinary and partial differential equations, like the Calculus of Variations, as well as numerical analysis will be learned and used in this project.

>Erika Norenberg is also in the REU, with a topic of "Morse theory and the topology of algebraic varieties."

The classical Lefshetz theorem implies that much of the topology of a smooth hypersurface in projective space is inherited from the ambient projective space. One of its standard proofs uses classical Morse theory, where the topology of a manifold is studied via critical points of a sufficiently generic function on it. A more general theorem, due to W. Barth, was proved in the early 1970's stating that smooth varieties of small codimension also inherit much of their topology from the ambient projective space. Barth's proof is rather complicated, but recently there is a new proof, due to Schoen and Wolfson, based on ideas of Gromov, based on Morse theory in infinite dimensions. Norenberg will work through Milnor's classic book on Morse theory and the Schoen-Wolfson paper. If time allows, she will study additional recent work generalizing these results and calculate some new examples.

David Eger sends his description of an REU into Aritifical Intelligence and Theorem Proving. As usual, he is well underway already!

(1) How can we use formal logic to codify typical mathematics in a machine verifiable form?

This exploration would start with filling in the holes in my knowledge of predicate calculus and using the program metamath (http://www.metamath.org/) to codify some basic proofs of theorems from Abstract Algebra. The basic pretense behind this project is that several large works (e.g. the Classification of the Simple Groups) are simply too large for any person to verify by hand and be absolutely sure he has not overlooked something. Codifying proofs and theorems in a database that is verifiable by a computer may offer us a valuable tool.

Also, I would like to see if I can codify some basic problems from combinatorics and the proofs their results. It always seemed rather bogus to me that someone would ask "Suppose you have a bus with one driver and fifteen students. There are twenty seats and one for the bus driver. How many valid sittings are there?" And with some hand waving one points out how many there must be. Perhaps this is the best we can do. But perhaps there is a proper natural symbolic representation we could have for this sort of problem. I could then contrast these attempts with the original problem and its solution. Does presenting a formal proof detract from understanding? Can we have our cake and eat it too: can we both have logic-level proof AND understanding? If so how? People tend to think in geometric manners; what geometric representations can be represented as alternatives to predicate calculus, and can such pictures be treated formally in provable, verifiable ways?

(2) Once we have a structure for representing logically our mathematics, can we use a computer to discern important properties and patterns about our mathematical objects, and if so how?

That is, in Abstract Algebra we have defined certain properties of operators which we find important in some way - commutativity, associativity, alternate associativity - from which many other "nice" properties follows. Are there less obvious properties from we might find in sets with operators that give us nice properties? What are the patterns that we see if we look at a selection of quasigroups? Can we use monte carlo methods to look for patterns which we might then put forward as hypotheses to then attempt to prove? Might we find things as important as Sylow's theorems in this manner? It's much of a "pi in the sky" question, but it's one that has perked my interest from time to time.

Alternatively I could try to construct a Theorem Proving System, which given certain truths, could try to deduce useful theorems. Embedding heuristics for "useful" could be quite a challenge.

(3) What do we want to do with computation? Why is it seen as such a fluid thing - practicing computer scientists commonly eschew the formal methods that seem to me essential? How could formal methods be applied to complex software systems, and what are the limits to such applications and why?

I would start this with a survey of texts both on Software proof systems such as Zed, some remedial reading on lambda calculus and functional programming, and a couple of texts on programming as a mathematical art, specifically, I'd like to explore Dijkstra's "A Discipline of Programming" and "Predicate Calculus and Program Semantics".

(3a) From this starting point I could draw material to try tackling what I believe to be an NP-Complete problem - a variant of the classical SAT problem called "Paint by Number", a pencil puzzle game which appeared in GAMES magazine in the 1990s. This I believe should take me on a journey through enumeration methods, some combinatorics, perhaps some graph theory, and in general should give me a good amount of ground to explore.

(3b) I could alternatively survey various software systems and with each ask the question "What elements of this system are (not) provably correct and why?" Which elements have simply ill-defined requirements; which are impossible to do correctly; which are trying to correct in some way for a break of an assumption of the programming model (out of memory conditions and other errors) and are these attempts misled in their nature, or useful?

Suppose for instance we are examining the halting problem and have written a program that determines whether a program will halt. Obviously such a program will not work for every program. But then, perhaps our program, by looking for certain signatures, will work, but only in a restricted subspace of the space of all programs. People often, I think, get caught in the rut that simply because the general case is impossible that the whole endeavour is hopeless.

Perhaps I will find that the vast majority of software has nothing to do with reality, since pre- and post- conditions are so rarely stated properly. The problem then may become, "What is the proper context within which we can look at the mathematically verifiable properties of our program?

Jeremy Barrett worked on the very difficult topic of graph theory that involves substantial interaction with finitely presented groups and an interplay with topology.

This topic was selected, in part by Jeremy himself, and was directed by Professor Xing-xing Yu. The time was spent trying to master a difficult book by Dunwoody, which is on this topic. In addition, Jeremy had some interactions with Computing grad students, and attended a short lived Morse theory seminar.

On the whole the topic, though close to Jeremy's interests, was too involved and sophisticated for him to gain a strong sense of satisfaction with the time he spent on the project. He, along with David Eger, wound up feeling a little isolated with their projects.

Summer 2001 REUs


Summer 2001 GT REUs
Professor	Student	Topic
Harrell	Clark Alexander	Convex Geometry
Heil	Nick Bronn	Time Frequency Analysis
Lacey	Nick Bronn	Sets avoiding Arithmetic Progression
Tetali	Blair Dowling	Elliptic Curves, Cryptography
Nagle	Erika Norenberg	Hypergraphs
Belinfante		Automated Reasoning

In addition, Patty Pichardo, David Eger, and Andrew Stimpson participated in off--campus REUs or internships.

Summer 2006 Outside REUs
Student	Outside REU
Anders Steele	PROMYS program
Alex Block	NSA Summer program
Nicole Larsen	Cornell Physics REU
AJ Friend	Penn State REU
Andy Tart	Cornell REU
Sarah King	SPWM, Georgetown
Mike Young	GTEAS REU
Michael Galvin	GT-Math Biology

Summer 2005 GT REUs
Professor	Student	Topic
T Trotter	Bill March
M Baker	Georg Steele
C Houdre/L Peng	Alex Block
E Croot	Brian Swanagan
M Baker	Matthew Tanzy
Y Wang	Charles Martin
P Mucha	AJ Friend
L Lefton	Darshan Bryner
Johan Belinfante	Claudia Huang
E Croot	Brian Williams
D Lubinsky	Ioana Soran
Y Liu + E di Lorenzo	Corina Saxon
Geronimo	Nick Cotton

Summer 2005 Outside REUs
Student	Outside REU
Robert Pruvenok	RIPS @ UCLA
James Sanders	Ithaca College
Thomas Callaghan	Park City Math Institute
AJ Friend	Park City Math Institute
Steven Lansel	Solar Car Challenge
Luke Snyder	National Security Agency

Summer 2005 Study Abroad
Student	Study Abroad
Adam Tart	GT/Oxford program
Matt Kurjanowicz	GT/Barcelona program
Steven Lansel	Argetina & Brazil

Research Experiences for Undergrads at Georgia Tech

2008 , 2007 , 2006 , 2005 , 2004 , 2003, 2001, 2002,

GT REU Summer 2008

Other activities/honors

GT REU Summer 2007